https://ojs.aaai.org/index.php/AAAI/article/view/5848
Introduction
PU Learningで選択バイアスが生じると、Class Priorの推定もずれてくる。ここでBiasの影響をできるだけ排した、Class Priorの推定をしたのがこの論文である。
この論文では、3つの重要な仮定を置き、その元での手法を開発した。
Background
- データはであり、ラベル空間はとする。
- 得られた分布は、ハイパーパラメタと、2つの分布によって、以下のように合成されたと考える。
- しかし、上の形だと一定に定まらないそうなので、以下のようにする。
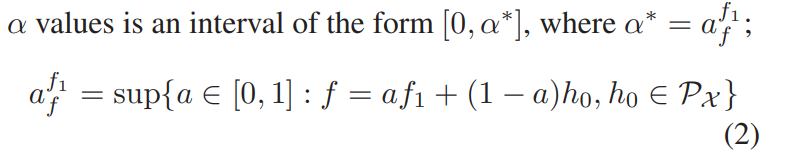
推測のやり方
この論文で基本にしてるのはAlphaMaxというアルゴリズムであり、nonparametricでclass priorを推測する。考えとしては、最適解の周りは急激に変化しているので、周りのGradientの変化が最も急なところを最適解とするというもの。
具体的には、何かしらの確率などにCalibrationされたに対して、を複数個のでサンプリングして、そこから曲線にあてはめて?曲がりが最大の変曲点を見つける感じ。
Theoretical Framework
考えている問題設定としては以下のようなもの。
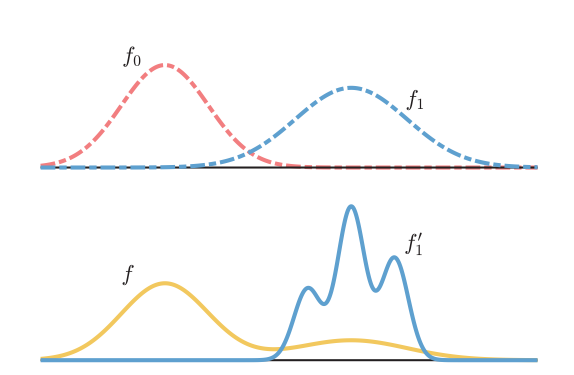
- Unlabeledの分布はであり、これはNegtaiveの確率分布とPositiveの確率分布を、ある割合で混合したものである。
- Positiveの分布であり、これは真のPositiveの確率分布とは違う=Biasedである。
定式化としては、以下のように何かしらの基底があるとして、は違う。
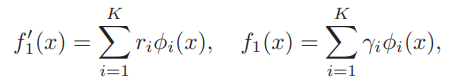
ある分布を構成する係数が一意になるように、φ irreducibilityという仮定を導入した。具体的には、Negativeは、非自明な基底φの合成で合成できないとしているらしい。
そのうえ、各Kernelの基底の台=supportは重ならないとも仮定。
Identifiability
ようわからん
もしはφ irreducibilityを持つ場合、ある分布に対して、係数の組成はユニークらしい。
Estimating Algorithm
Biased PU Dataを複数個のUnbiased PU Dataに分解し、そこからAlphaMaxのアルゴリズムを使いたい。最後に分解した各データからの情報を統合したい。
- データセットを個の集合に分割する。これはk-meansなどのクラスタリングアルゴリズムを使う。
- この手法では、まずPositive Dataについてk-meansで分割する(シルエット係数というものを最大化するようなを選ぶらしい)。
- 次にUnlabeledを、すでに計算されたクラスタの中心との距離に基づいて分割する。
- 各集合について、何かしらのSupportがお互いかぶらないKernel基底の分布に従うとする。
- Positiveデータは、Kernel基底の分布に従って生成されるとする。
- はお互いに台がかぶらないというが、k-meansでクラスタリングしている以上、割り当てられたエリアのデータしか生成しないので、確かに台がかぶらないという前提からクラスタリングという発想はわかる。
- Unlabeledデータは、別の分布に従う。
- つまり、各は、の合成分布によってサンプリングされる。
- Positiveデータは、Kernel基底の分布に従って生成されるとする。
- 、。
- は全体の中で占めるの個数の割合。
- なので、は、全体の中でのに従うものの割合である。
- これに従う各分布で合成すれば、Positiveの推定分布になる。
- はのUnlabeledのデータで、に対応しない残りの部分を示す分布。
- これに従う各分布で合成すれば、Unlabeledの推定分布になる。
- これらで推定すると、以下のようになる。
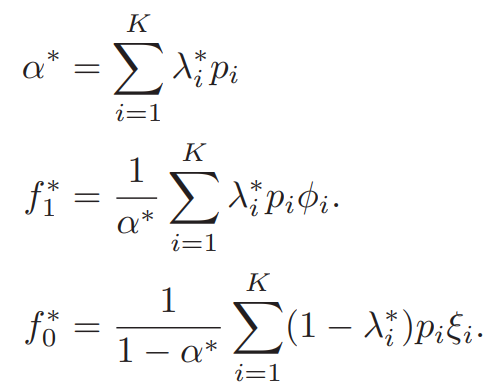
一番求めたいの推定は、が必要で、k-meansで各クラスタに分ければ、前者はAlphaMaxで推定でき後者もおのずとわかる。そしてついでにも、データから分布を(パラメトリック、ノンパラメトリック問わず)推定できれば、おのずとわかるかんじ。
アルゴリズムとしてはこんな感じである。

